[확률 및 통계] 기초 개념 정리 ②

모수(Parameter)

• 미지의 확률 분포에 대한 성질, 평균(=μ), 분산(=σ^2) 등
• 모수는 일반적으로 알려져있지 않음

모수 추정(Parameter Estimation)

• 추출된 sample data로 모수를 예측하는 것으로 크게 점추정과 구간추정으로 구분됨

점추정

• 모수를 하나의 값으로 추정하는 것
• 모평균 μ의 점추정량 : 표본평균 x̅

• 모분산 σ^2 의 점추정량 : 표본분산 S^2

• 추정량(estimator) : 수치가 아닌 일종을 절차
• 추정치(estimate) : 절차에 실제 표본 값을 대입한 수치

신뢰구간의 의미

신뢰구간의 종류

모평균의 신뢰구간

• 모분산을 아는 경우 양측 신뢰구간
  • 평균 μ, 분산 σ^2인 정규분포를 따르는 모집단으로부터 n개의 표본을 추출하면 표본평균 x̅와 이를 표준화 한 Z는 아래의 분포를 따름

• 모분산을 아는 경우 단측 신뢰구간

• 모분산을 모르는 경우 양측 신뢰구간

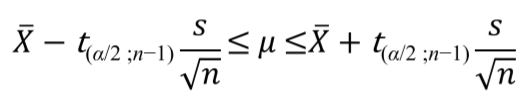
• 모분산을 모르는 경우 단측 신뢰구간

가설검정(Hypothesis test)

• 모수에 대한 가설을 세우고 표본을 추출하여 가설의 진위를 판단하는 과정

가설 설정

• 귀무가설(Null hypothesis : H0) : 기존에 알려져 있는 값, 모수를 하나의 값으로 정의, 가설 검정 과정 동안 참값으로 가정

• 대립가설(Alternative hypothesis : H1) : 귀무가설에서 제시한 값을 제외한 나머지 영역에서 모수의 값으로 정의

가설 검정의 원리

• 귀무가설이 옳다고 가정하고 검정 통계량을 계산
• 가설 검정의 기본 원리 : 모순에 의한 논증법(Argument by contradiction)
  • 귀무가설이 주장이 옳다면 어떻게 자료상으로 그렇게 극단적인 값이 나타날까?
  • 귀무가설이 틀리지 않고서야 어찌 이런 일이??! 라는 물음에서 시작
• 귀무가설이 옳다는 가정하에 계산된 검정 통계량이 극단적인 값의 범위(=기각역)에 포함되면 귀무가설 기각

가설 검정에 의한 오류

• 제 1종 오류 : 귀무가설이 참인 경우 귀무가설을 기각하는 오류
• 제 2종 오류(=β) : 귀무가설이 거짓인 경우에 귀무가설을 기각하지 못하는 오류
• 유의 수준(=α) : 허용 가능한 제 1종 오류, 통상적으로 1% 혹은 5%로 설정, 기각역 설정의 기준이 됨
• 검정력(=1-β) : 귀무가설이 거짓일 떄 이를 기각할 확률
• 다른 조건이 동일하다면, 유의수준과 검정력은 상충관계임

모평균의 검정

모분산의 검정

두 모분산 비의 검정

두 모평균 차이의 검정

검정과 신뢰구간의 관계

• 검정에 의한 판정과 신뢰구간에 의한 판정은 모수의 추론이라는 점에서 성격이 동일함
• 신뢰구간이 귀무가설의 모수를 포함하고 있으면 귀무가설을 채택함